Pressing questions I have:
- Why so many stacked blocks? What motivated the specific dimensionality and architecture? I know it inevitably involved a lot of research, and learning about neural networks and what works in practice; but what is the intuition behind using this specific amount of blocks in this order for both the VAE, and the U-NET?
Scratch Stable Diffusion Model

I’m making this page purely to aid in my own understanding, and should not be taken seriously as an ‘educational resource’
TO-DO: make an image of the video-generation model that you want to eventually create; and have this as a little-bit of a long-term project your looking forward too!
With this page, I hope to explore, and understand the motivations behind the architecture of the Stable Diffusion Model, and what motivated it, because:
- It is a fun and fascinating technical implementation, and is completely open-source
- The images are beautiful, and similar models will inevitably be used to revolutionize our world
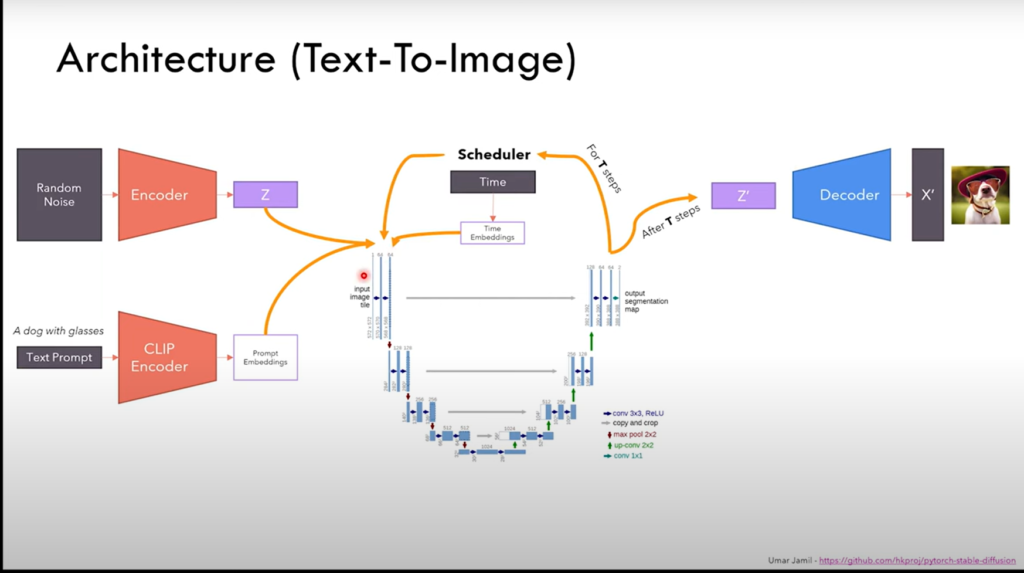
Step 1: Building-out with pytorch
Before going into the history and motivations of the model, I hope to be able to dig in, and completely understand, on a relatively low-level, everything that makes up the architecture, and why it works.
In this step I will abstract away to backpropagation and operations like convolutions, normalizations, and optimizations with Pytorch, as I already feel I have a good enough knowledge, and could implement these from scratch.
If I am lacking understanding in any spot, or my curiosity takes me to explore something more in-depth, I will do so.
Notes:
- How they built the architecture (copied some stuff)
Group-Normalization

Group normalization can effectively be seen as a compromise that has been observed to work in practice.
It involves grouping a specified amount of channels of feature-maps, and normalizing these channels (mean 0, std. 1). This means that while groups of features preserve independence, we still have very stable distributions that are not influenced by the mini-batch.
Normalization
Normalization allows the elegantness of normally distributed numbers for our network. If we let our network go unconstrained, it would not learn that 1 (std. deviation) is a ‘meaningful’ change in an output, and that 0 is a normal/ unexpressive. If we did not have this, it could be on a very-small, or very-large scale.
Convolutional Layers
Scan images, are more efficient because look for larger features, which individual connected neurons cannot do.
Residual Layers
Create gradient highway. each layer works on thing.
Attention Blocks
After convolutional layers are working-through, we will have many low-dimensional feature-maps. We re-group these feature maps, so each similar pixel as per it’s coordinates takes all the features maps’ values as its embedding, and it attends to all the other pixels!
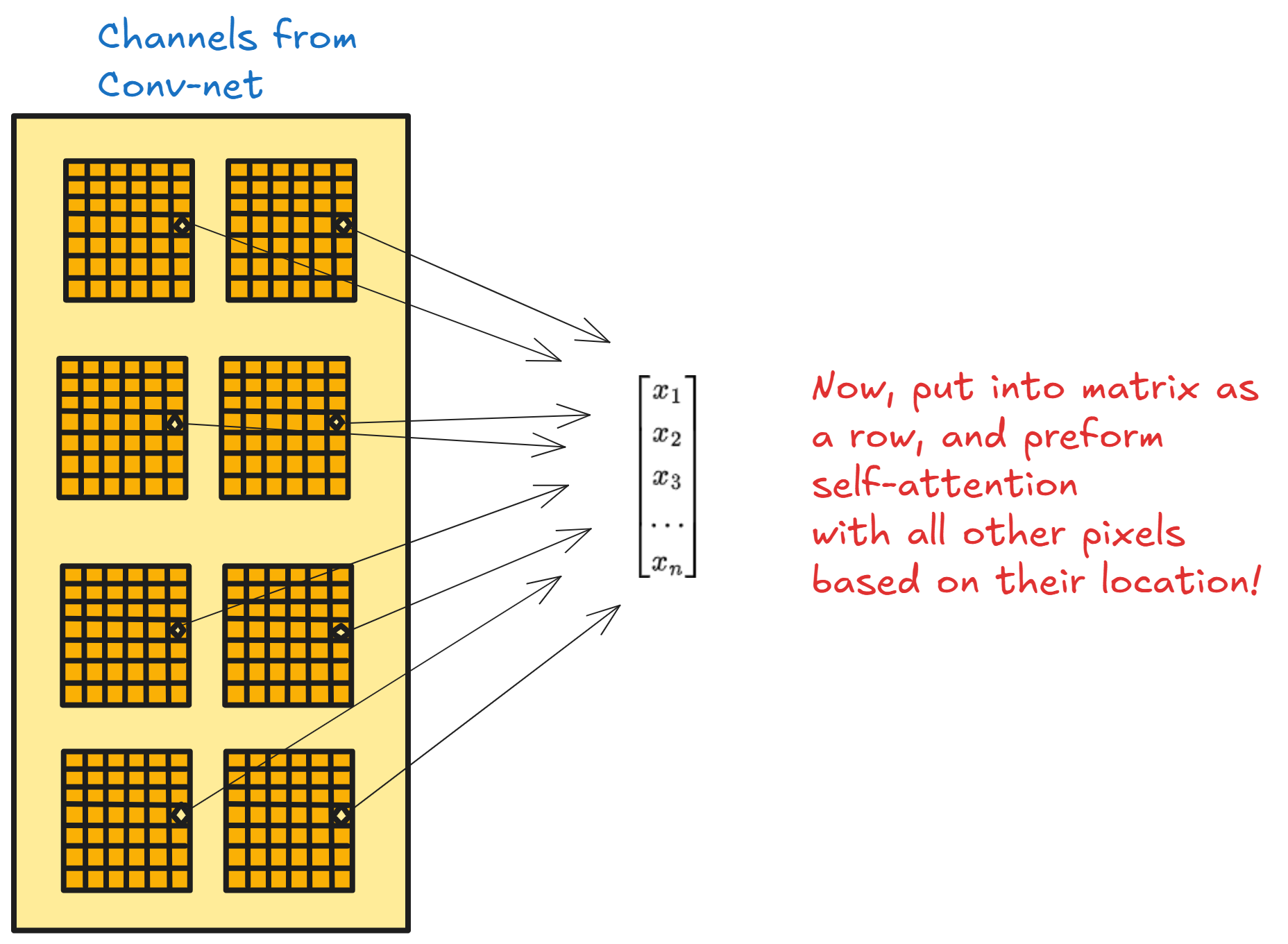
Self-attention for pixels was originally introduced add-source-here, and can work for pixels, because:
Up-Sampling
We do this in our decoder to increase the dimensions. After multiple convolutional (residual) blocks that preserve the shape with many feature-maps, we project our pixels simply to a higher dimension.
ups = nn.Upsample(scale_factor=2)
ups(tensor_1)
This effectively will multiply each element to span one down, and one to the right of itself, growing the height and width by 2. We use this simply to grow the dimensionality, and then continue to try to build the image with the decoder.
Overall structure of VAE
The overall structure of our VAE, is simply having expressive convolutional layers with residual connections for stability, and attention blocks for the image to know ‘what it is’ relative to the other pixels (think VIT architecture)
CLIP
Since we are just downloading the weights, we don’t need to worry about fully training a CLIP model, however we go more in-depth into the clip architecture here. Basically, our CLIP is just a transformer model that is has already been trained to align arbitrary text with any image.
The reason we are using CLIP to feed into our UNET, is because CLIP models are trained especially to represent images from text form, so even if we don’t match the latent-space exactly of the VAE, we still have something that is more descriptive for images, and therefore will help us denoise our image better.
Another important thing, is that our CLIP model is fixed at 77 tokens. We can only input this much, and if we input any less, our text is ‘padded’ effectively meaning the model will realize these tokens are useless.
U-NET/DDPM
Find my explanation of DDPM maths here
Basically, given some text, a timestep, and the latent-vector, the UNET must learn to denoise the latent-vector.
- The UNET implements residual connections that actually skip between multiple layers of blocks, so we can learn something definitively as we compress the image, and allow the gradients to flow further.
- Our Unet will take in both an image and a text vector, along with the timestep that it has to denoise with. These will be kept as separate channels, although cross-attention will be used across the two vectors.
Our U-NET is trained WITH text embeddings from the transformer (clip), so it will learn to denoise image with help from the embeddings. This is key, because we can eventually train the model to generate images from scratch with just noise and the text embedding.
Interestingly, the text embedding is not just for the prediction of the next token, as although theoretically this sums up our entire sequence, it gives the model more fine-grained control to access contextual information for all the tokens. This may be because different information is important for images, and it is better to give the information to UNETs in this way.
Skip Concatenation
Another interesting part of the U-Net architecture, is that it implements its skip-connections by concatenation to the channel-dimension. This allows the decoder in subsequent layers to select from both the original image, and the current step of rebuilding: allowing for an easier task in rebuilding, rather than having a the skip-connections just added to the pixel-values.
This can also be phrased as: preserving the original encodings to have to compare and use with the deeper embeddings that we develope in the encoder.
Cross-attention
The U-Net is actually only processing the latent-vector; the CLIP tokens, and time-embedding do not change, and are used to aid the denoising process throughou the unet.
Cross-attention is how the latent-image vector learns from the CLIP context:
- The keys and values are generated from the context
- The queries are generated from the current latent-space-state
- We preform this attention, and obtain a new latent-space
Architecture/Training
An important part to note about this model, is that the parts are trained separately. The CLIP model is trained separately, and the VAE is trained to reconstruct and deconstruct latent-codes, and finally, the UNET is trained to denoise these latent-vectors that were generated by the VAE.
This allows for training stability, and we could swap out different UNETs with the same trained VAE and clip.
Pre-activations
It was found in this paper, that having activation functions before convolutional layers in Res-Net conv. blocks achieved better training. More research necessary into this
Geglu
The Geglu activation function, has two sets of weights: one part of the output acts as a ‘gate’ under the GELU function (outputs between zero and one), and other outputs are the ‘raw’ linear outputs. This allows more expressivity, as in theory a network could learn very expressive outputs in the linear layer, and selectively control them with the GELU gate.
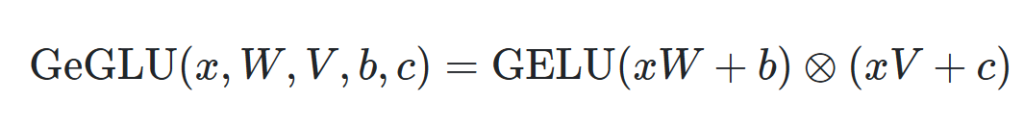
Pipeline: Putting things together
The pipeline involves constructing a ‘scheduler’ which informs the UNET at what step it is in removing the noise, and then simply feed the UNET some CLIP embeddings, and some noise! We don’t have to worry about training, or loss objectives; we will cover this more in-depth as this is the true important part about building these models. I will investigate this more on my diffusion page.
EMA weights/ downloading weights
We will download the ‘Exponential moving average’ weights which are basically the state of the weights averaged over the entire dataset, while the regular weights are the last-state of the model. EMA weights tend to be more stable and representative, but for fine-tuning EMA must not be used to allow for rapid change in parts of the model that is necessary.
We will also need to download a tokenizer: which takes our raw text and converts it into tokens.
Classifier-Free guidance
In inference, we have something called classifier-free guidance, where we allow at each de-noising step the model to denoise both the image by itself and the image with the prompt, and then we add it like this:
guided = prediction_without + w*(prediction_with - prediction_without)
this is applied at each denoising step in the U-Net, and represents how much we want to follow strictly what our prompt says vs. some other probabilistic output of the denoising process.
Negative prompt
The same concept works if we decide to use a negative prompt. We subtract the normal-guided vector with the negative vector which acheives some sense of the ‘opposite direction in latent-space’. The fact that this works amazes me.
LOOK IN MORE TO THIS: HOW DOES SUBTRACTION WORK IN UNET?
Strength
The strength parameter determines how much noise we add to the input image (if we decide to give one), and more noise means the model has more denoising to do, and therefore will be more creative.
Image generation
Now, given a text prompt(s), an input image (optional) and some noise, the model takes the noise from step T, to step zero, skipping steps as to speed up the process.
The model has learned to denoise from any arbitrary timestep to timestep 0. However, when we preform inference, we purposely remove only allow the model to move a small amount of noise, which results in more detailed images. This makes sense, because the model is able to gradually predict the probability of the next image and ‘think’ more about what it should be.
Sampler (the crux of inference)
Our sampler given the number of total timesteps, and given how many we specify to iterate through, will be tasked with de-noising the image only partially, and feeding this along with the appropriate embedding back into the model.
Here is the overall process (with classifier-free guidance):
- We re-shape our input image (optional) and pass it through the encoder (VAE), and then pass our tokens through our CLIP language model: an empty string and our text prompt.
- Noise our image in the latent-space, and then pass it through our U-net with the embeddings (2 separate batches) and the time-embedding (determined by scheduler), and add the conditional and unconditional outputs according to our weight.
- Remove only a bit of noise (restricted by scheduler), and pass it back through the model with the next timestep
Positional embeddings
Our scheduler has to give positional embeddings for our timesteps, which our model then linearly projects as part of the UNET.
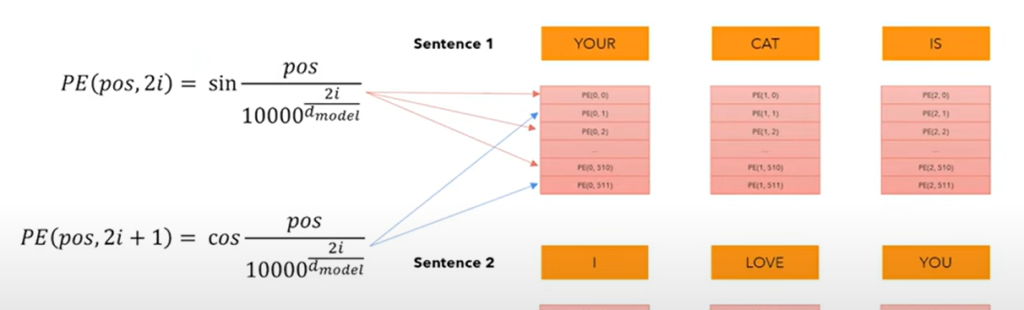
We use this formula, as over time it is found that the embeddings converge to sin/cos waves even if we just learn them.
The intuition behind this is as follows:
- we want to express something different in each dimension (hence lower-frequencies in different dimensions), and we also want the embeddings themselves to vary. This is a simple way to do this.
- Since we alternate between sin and cos, when one is changing rapidly, the other is changing slower
- relative distance throughout sequence maintained
Time embeddings
We do time embeddings with the same formula as above, just with different dimensionality.
Beta Scheduler
Our beta scheduler is the schedule for our noise. Remember, we gradually add noise to our image, transforming it into a gaussian, this process is parameterized by:
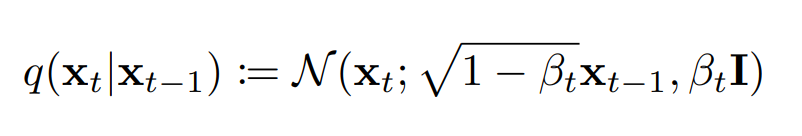
which we set a schedule for β. We set a start and end β, and since we want to progressively add more noise, the end is greater. We progress with a linear schedule, but other schedules can be use, as long as they gradually denoise in a somewhat stable way.
So, for 1000 steps we could simple define our betas as:
betas = torch.linspace(beta_start**0.5,beta_end**0.5,1000)
and we take the square root so the standard deviation scales linearly, which is a choice by the creators that may offer stability.
Sampler
Let’s continue to look at our sampler; now that we have all of our beta’s known, we can calculate an arbitrary timestep q, simply by exploiting the continual-gaussian nature of the noising process:
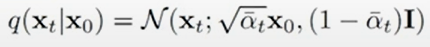
and since we know this, given our predicted noise from our U-Net, we can ‘jump’ to any arbitrary timestep! And since we’ve already defined beta, we can easily find alpha bar, which is just the product of alphas (1-beta).
So, we set our standard-deviations to vary linearly, and then we convert this to our alphas, which we will actually be using in our computations for calculating the t’th image we are on, given the models prediction of the noise.
We can define this as follows:
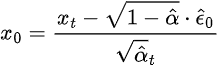
we basically sample this, and then plug it into the formula given here, I tried a simple formula, but it did not end up working 🙁 RE-TRY
This could be interpreted as “being in a foggy forest, and predicting where the exit is, taking a step, and then modifying your prediction after you take the next step”.
This is interesting, and we should explore it more.
While our distributions are multi-dimensional, our alpha’s stay constant across dimensions, because they are simply guiding the noising process and making sure it is stable.
De-noising our image
Again, to denoise our image and go to the next-step, we predict the original noise and plug it back into our formula shown above q(x_t | x_0). Then we ‘jump’ to the next step, and find q(x_n | x_0) by putting x_0 in terms of noise and x_t.
Setting strength of diffusion
When we set the strength with integers [0,1], we specify how much we want the denoising process to pay attention to the original image, where a high strength is very little attention paid.
Basically what we do, is advanced the denoising process the percentage of (1-strength), and add noise to the corresponding step accordingly. This is equivalent to ‘tricking’ the model into thinking it created the previous steps, when in reality it was us that inputted the image.
Different number of diffusion steps
Let’s look at what it looks like when we use different numbers of steps in our diffusion process! Remember, multiple steps can be seen as iteratively moving a small amount of noise, and then adjusting based on this. Also, we remove more noise at early steps, because of increasing std. dev., so we will have the most rapid changes at the beginning.
Loading the weights from 🤗
Now, we load the weights so we can finally preform inference! This is simple; all we need to do is apply the weights to our pytorch model and make sure that the names match. We can just use pytorch’s “load_state_dict” for each model-class.
Unfortunately, our clean code does not match the actual state-dict of the weights by name. Therefore, we need a long function that creates a new dictionary with new names and converts each original key to a new key friendly to our code. This is common when loading models.
Future projects.
I’ve learned a lot from this implementation of stable-diffusion, it was my first project in a while, so i made a lot of mistakes.
- Stay organized: clear goal for project
- Have a goal for your project
- Have a way to test your code!
- Keep your learning as you go organized in one place!
- Operate somewhat independently
- Have your own idea for your project so you can really implement something from scratch
- But still have something to follow for inspiration