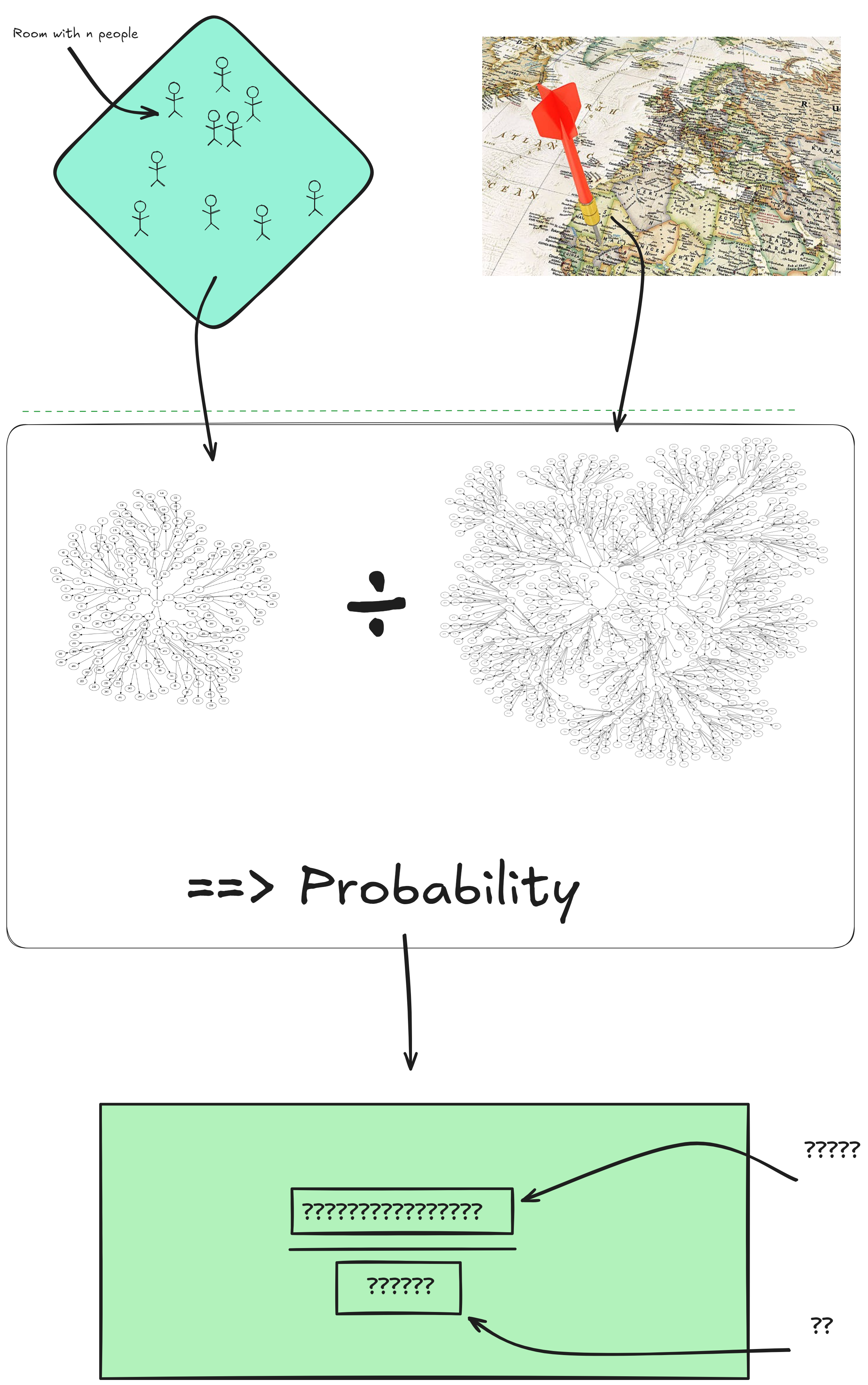
Birthday Probability Problem: A Geometric Approach
Lets solve the problem: how many people in a room does it take
for it to be more likely than not that at least someone shares a birthday with another?
Reason:
This simple problem offers a lot of intuition into what Probability
actually involves, and uses fundamental methods to find a solution.
Also I want to show a pretty neat geometric intuition 🙂
Pt.1 Branching
The first thing I would like to discuss is the geometric interpretation
of ‘counting’ the number of ways something that can happen.
Lets look at a simple coin flip first.
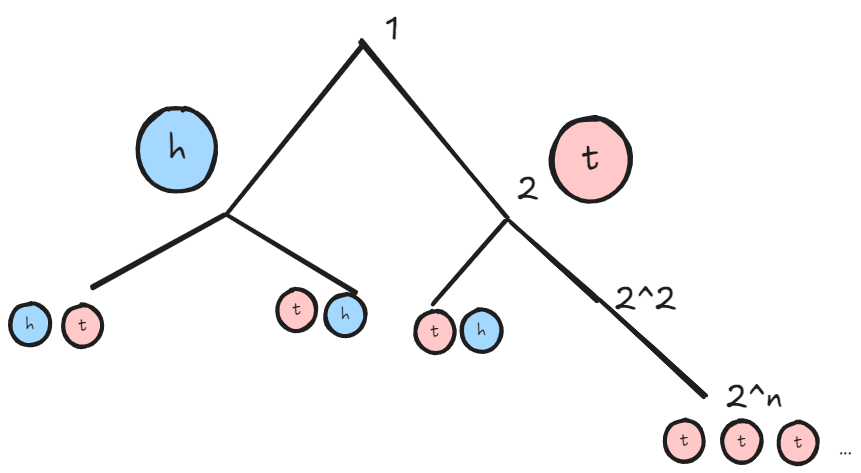
Above we can see that if we have 2 possible outcomes, as we preform more actions,
or flip more coins, the number of possible outcomes (represented by each branch) grows
exponentially. Each branch has two more branches, and so on.
This extends to any system with a finite number of outcomes, and we will soon
see that it is one of the key intuitions for our birthday problem.
There are two more things we’ll need to understand before we can move forward in our problem.
1. Replacement
2. Order
Replacement is simple, it means that for each consecutive branch, there will be one less possibility.
Think of a drawing cards from a deck: originally we have 52 branches, but the second branch will only be 51
because we have exhausted one of our possible outcomes (we didn’t replace). The formula for this is: n*(n-1)*(n-2)…*2*1 ==> n!
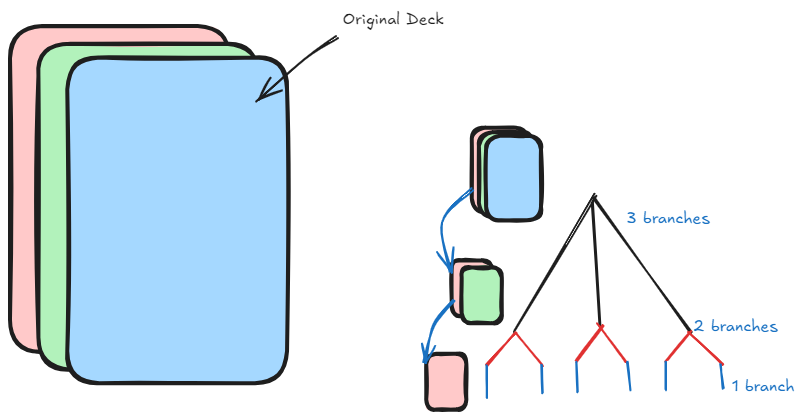
Our branches are basically for the purpose of counting the number of possible outcomes
when doing something n times. What if I want to count the number of possible hands I can
have in poker (where order doesn’t matter)? In this case, we divide the number of possible outcomes
by the number of possible ways we could arrange our hand (note that this only applies for no replacement).
Here is an intuition for how we calculate the number of combinations of something:
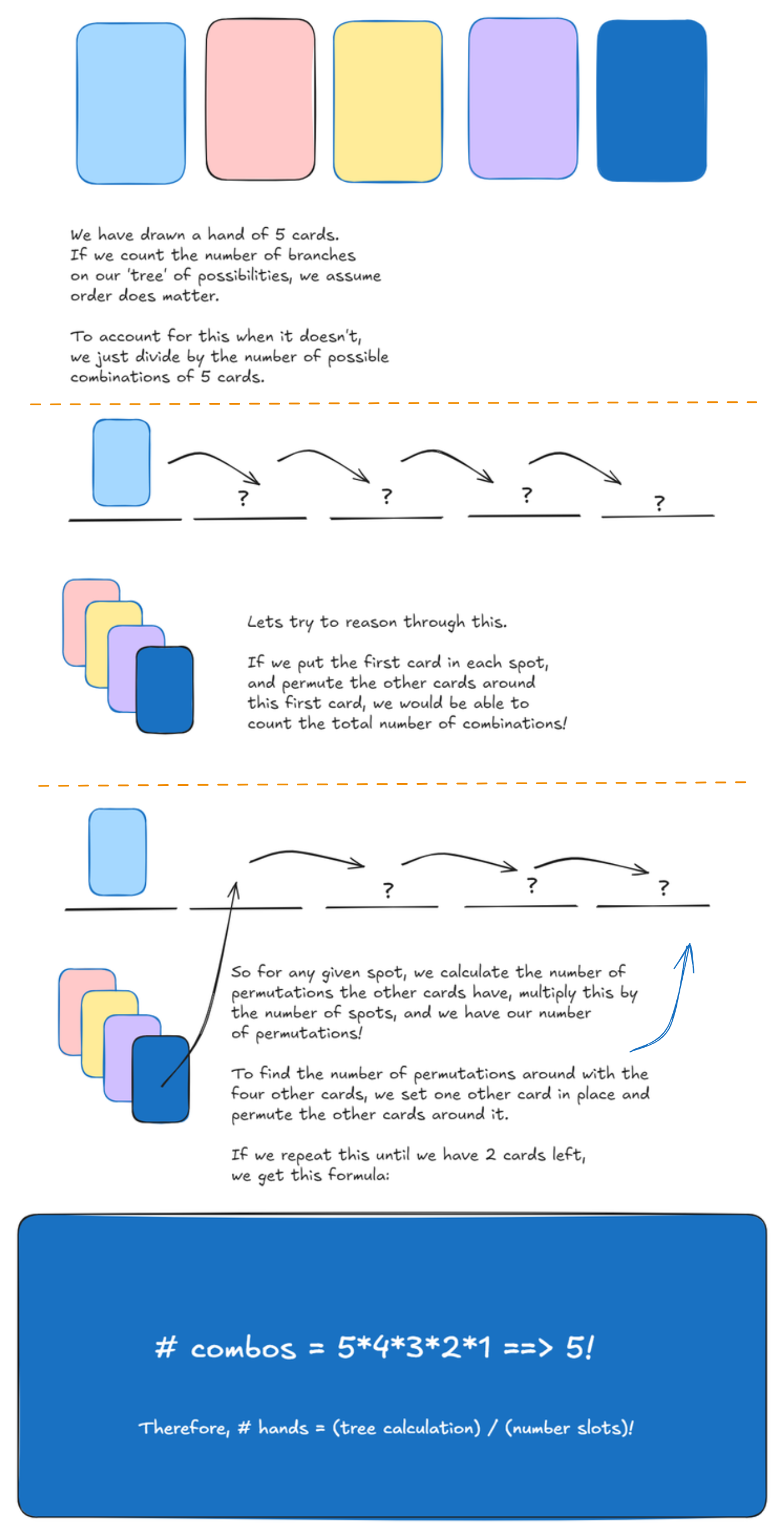
And if you haven’t already figured out, the formula for counting total outcomes
without replacement is n!/(n-r!) (where n is number of possible outcomes at the start, r is
the number of branches out). This basically is just the way that we get 65*64*63…
instead of exponentiating.
Pt.2 Probability as area
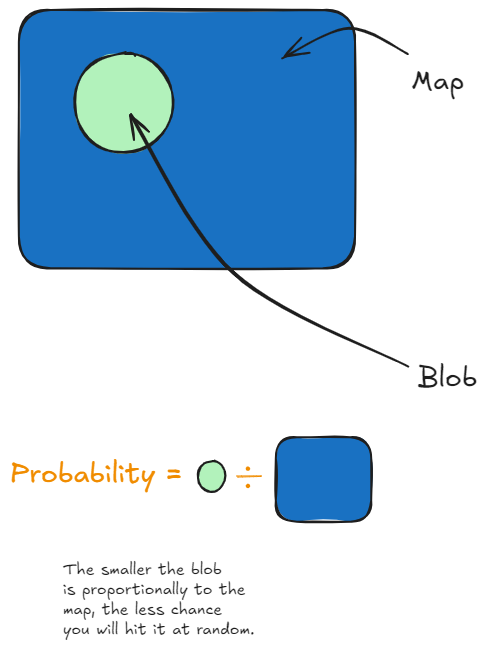
Imagine you throw a dart onto a map, blindfolded. The spot
you will hit on the map is completely random. If I have a
country on the map, intuitively, the larger it is the more likely
you are to hit it. We can think of this as a ratio of:
the size of the map / the size of this blob
if the blob is half the size of the map, you have a 50% chance
of hitting it, and the same goes for any other ratio.
This actually extends to all other problems involving probability
of an event occuring.
Now, there one last thing to understand before we tie this to our
birthday problem.
If we have an ability to count how many possible outcomes there are for a given
event, and also count how many times a specific outcome occurs,
we can use the ‘proportionality’ to deduce the probability that an event occurs,
by simply diving the number of desired outcomes by the number of total
possible outcomes.It is clear to see how this is directly related to our map issue.
Lets see a very simple example by going back to our coin flip:
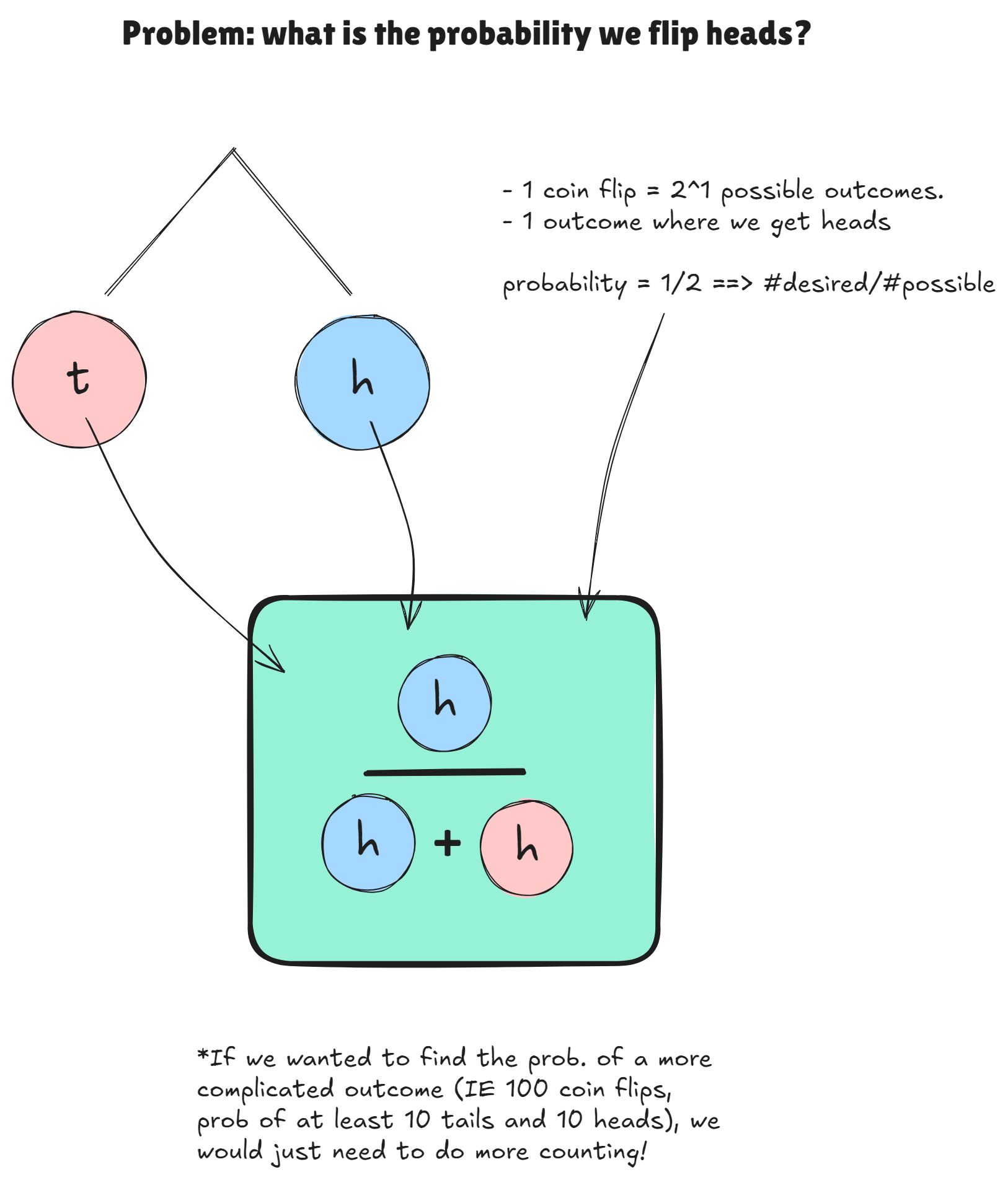
Also note that we assume that heads and tails are equally
likely. If they weren’t, we would just make one of their
areas bigger. Similarly in our problem, we will assume that
every birthday date is equally likely.
The Grand Finale: Applying our methods
Now that we know how to count the number of outcomes for something
happening, and we know how to get probability based on this,
we can solve our problem.
Step 1 is counting the number of possible birthdays in a room with n people.
Step 2 is counting the number of ways that n people can
share a birthday.

So, there is our answer! We have come up with the formula,
so now for the easy part: getting the actual number.
We’ve essentially come up with a way to calculate the chance that
no one shares a birthday, so we’ll calculate this in a loop until
the chance is less than 0.5 out of 1. Then, we have our magic number
that tells us when it is more probable than not that n people in a room share a
birthday!
Leave a Reply